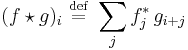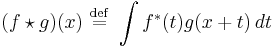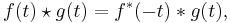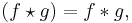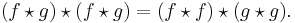Cross-covariance

In statistics, the term cross-covariance is sometimes used to refer to the covariance cov(X, Y) between two random vectors X and Y, in order to distinguish that concept from the "covariance" of a random vector X, which is understood to be the matrix of covariances between the scalar components of X.

In signal processing, the cross-covariance (or sometimes "cross-correlation") is a measure of similarity of two signals, commonly used to find features in an unknown signal by comparing it to a known one. It is a function of the relative time between the signals, is sometimes called the sliding dot product, and has applications in pattern recognition and cryptanalysis.

1 Statistics
2 Signal processing
- 2.1 Properties
3 See also
4 External links

Statistics

For random vectors, X and Y, each containing random elements whose expected value and variance exist, the cross-covariance matrix of X and Y is defined by

$\operatorname{cov}(X,Y)=\operatorname{E}[(X-\mu_X)(Y-\mu_Y)'],$

where μ_X and μ_Y are vectors containing the expected values of X and Y. The vectors X and Y need not have the same dimension, and either might be a scalar value. Any element of the cross-covariance matrix is itself a "cross-covariance".

Signal processing

Main article: Cross-correlation

For discrete functions f_i and g_i the cross-covariance is defined as

$(f\star g)_i \ \stackrel{\mathrm{def}}{=}\ \sum_j f^*_j\,g_{i%2Bj}$

where the sum is over the appropriate values of the integer j and an asterisk indicates the complex conjugate. For continuous functions f (x) and g (x) the cross-covariance is defined as

$(f\star g)(x) \ \stackrel{\mathrm{def}}{=}\ \int f^*(t) g(x%2Bt)\,dt$